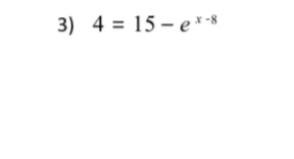AI tutor
Full solution
Q.
- Isolate Exponential Term: Step Title: Isolate the Exponential TermConcise Step Description: Add to both sides to isolate the exponential term on one side of the equation.Step Calculation: Step Output:
- Subtract : Step Title: Subtract from Both SidesConcise Step Description: Subtract from both sides to get the exponential term by itself.Step Calculation: Step Output:
- Take Natural Logarithm: Step Title: Take the Natural Logarithm of Both SidesConcise Step Description: Apply the natural logarithm to both sides to solve for .Step Calculation: Step Output:
- Add : Step Title: Add to Both SidesConcise Step Description: Add to both sides to solve for .Step Calculation: Step Output:
More problems from Factor polynomials
QuestionGet tutor help
QuestionGet tutor help