Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

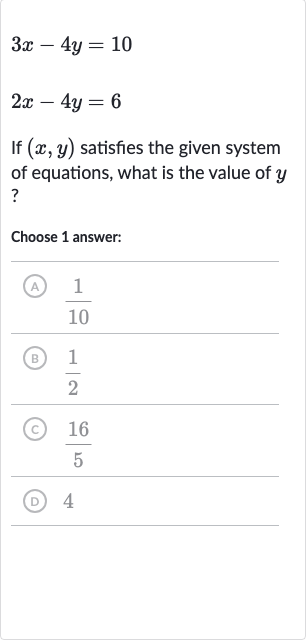
3x-4y=10

2x-4y=6
If
(x,y) satisfies the given system of equations, what is the value of
y ?
Choose 1 answer:
(A)
(1)/(10)
(B)
(1)/(2)
(c)
(16)/(5)
(D) 4

$\begin{array}{l} 3 x-4 y=10 \\ 2 x-4 y=6 \end{array}$ $\newline$ If $(x, y)$ satisfies the given system of equations, what is the value of $y$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{1}{10}$ $\newline$ (B) $\frac{1}{2}$ $\newline$ (C) $\frac{16}{5}$ $\newline$ (D) $4$

View step-by-step help

View step-by-step help

Domain and range

Full solution

Q.

\begin{array}{l} 3 x-4 y=10 \\ 2 x-4 y=6 \end{array}

\newline

If

(x, y)

satisfies the given system of equations, what is the value of

y

?

\newline

Choose

1

answer:

\newline

(A)

\frac{1}{10}

\newline

(B)

\frac{1}{2}

\newline

(C)

\frac{16}{5}

\newline

(D)

4

Equations: We have the system of equations: $\newline$ $3x - 4y = 10$ ( $1$ ) $\newline$ $2x - 4y = 6$ ( $2$ ) $\newline$ To find the value of $y$ , we can subtract equation ( $2$ ) from equation ( $1$ ) to eliminate $y$ .
Eliminating y: Subtracting equation ( $2$ ) from equation ( $1$ ) gives us: $\newline$ $(3x - 4y) - (2x - 4y) = 10 - 6$ $\newline$ This simplifies to: $\newline$ $3x - 2x = 10 - 6$
Simplifying equation: Simplifying the above equation gives us: $\newline$ $x = 4$ $\newline$ Now we have the value of $x$ .
Finding x: Next, we substitute the value of $x$ back into one of the original equations to solve for $y$ . We can use equation ( $2$ ) for this purpose: $\newline$ $2x - 4y = 6$ $\newline$ Substituting $x = 4$ gives us: $\newline$ $2(4) - 4y = 6$
Substituting $x$ into equation: Solving the above equation for $y$ gives us: $\newline$ $8 - 4y = 6$ $\newline$ Subtracting $8$ from both sides gives us: $\newline$ $-4y = 6 - 8$
Solving for y: Simplifying the above equation gives us: $\newline$ $-4y = -2$ $\newline$ Dividing both sides by $-4$ gives us: $\newline$ $y = \frac{-2}{-4}$
Final value of y: Solving the above equation for y gives us: $\newline$ y = $\frac{1}{2}$ $\newline$ So the value of y is $\frac{1}{2}$ , which corresponds to choice (B).

More problems from Domain and range

Question

What is the domain of this function?

\newline

(9,–2)(6,–10)(–3,9)(5,2)

\newline

\newline

(A)\{–3,5,6,9\}\newline(B)\{–10,–2,2,9\}\newline(C)\{2,5,6,9\}\newline(D)\{–6,–3,5,9\}

Posted 1 year ago

Question

Look at this set of ordered pairs:

\newline

(2, 14)

\newline

(10, 12)

\newline

(3, -19)

\newline

Is this relation a function?

\newline

\newline

\text{[[yes]}

\text{[no]]}

Posted 1 year ago

Question

Use the following function rule to find

f(11)

\newline

f(x) = -10 - 7x

\newline

f(11) =

Posted 1 year ago

Question

Find the slope of the line

y = -3x - \frac{2}{5}

\newline

Simplify your answer and write it as a proper fraction, improper fraction, or integer.

\newline

\_\_\_\_\_

Posted 1 year ago

Question

A line has a slope of

3

and passes through the point

(-2,-10)

. Write its equation in slope-intercept form.

\newline

Write your answer using integers, proper fractions, and improper fractions in simplest form.

Posted 1 year ago

Question

What is the range of this function?

\newline

\newline

\newline

\text{all real numbers}

\newline

\{y \mid y \geq 0\}

\newline

\{y \mid y \leq 0\}

\newline

\{y \mid y > 0\}

Posted 1 year ago

Question

g(x)

g(x)

is the translation

1

f(x) = |x|

\newline

Write your answer in the form

a|x - h| + k

a

h

k

\newline

g(x) =

\newline

Posted 1 year ago

Question

What is the domain of this function?

\newline

(8,–1)(7,–11)(–4,10)(4,3)

\newline

\newline

(A)\{–4,4,7,8\}\newline

(B)\{–11,–1,3,10\}\newline

(C)\{3,4,7,8\}\newline

(D)\{–7,–4,4,8\}

Posted 1 year ago

Question

What is the domain of this function?

\newline

(10,\,–3)(2,\,–9)(–5,\,8)(3,\,1)

\newline

\newline

[\{–5,2,3,10\}][\{–9,\,–3,1,8\}][\{1,2,3,10\}][\{–10,\,–5,2,3\}]

Posted 1 year ago

Question

What is the domain of this function?

\newline

(1,–4)(9,–12)(–6,11)(7,5)

\newline

\newline\\(A)\{–6,1,7,9\}\newline

(B)\{–12,–4,5,11\}\newline

(C\{5,1,7,9\}\newline

(D)\{–9,–6,1,7\}

Posted 1 year ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant