Full solution
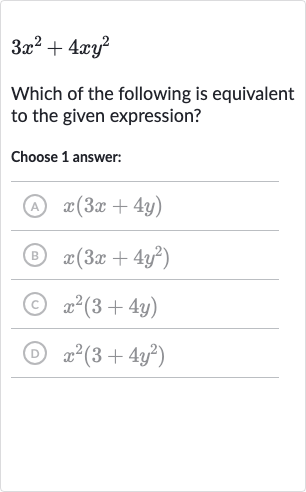
Q. Which of the following is equivalent to the given expression?Choose answer:(A) (B) (C) (D)
- Identify Common Factors: To find an equivalent expression, we need to look for common factors in each term of the given expression .
- Factor Out Common Factor: The first term is , which has a factor of . The second term is , which also has a factor of . Therefore, is a common factor in both terms.
- Compare with Options: We can factor out the common from both terms to get .
- Compare with Options: We can factor out the common from both terms to get .Now we compare the factored expression with the given options to find the equivalent expression.
- Compare with Options: We can factor out the common from both terms to get .Now we compare the factored expression with the given options to find the equivalent expression.Option (A) is , which is not equivalent because it does not have the term in the second part of the expression.
- Compare with Options: We can factor out the common from both terms to get .Now we compare the factored expression with the given options to find the equivalent expression.Option (A) is , which is not equivalent because it does not have the term in the second part of the expression.Option (B) is , which is equivalent to our factored expression.
- Compare with Options: We can factor out the common from both terms to get .Now we compare the factored expression with the given options to find the equivalent expression.Option (A) is , which is not equivalent because it does not have the term in the second part of the expression.Option (B) is , which is equivalent to our factored expression.Option (C) is , which is not equivalent because it suggests that both terms originally had an factor, which is not the case.
- Compare with Options: We can factor out the common from both terms to get .Now we compare the factored expression with the given options to find the equivalent expression.Option (A) is , which is not equivalent because it does not have the term in the second part of the expression.Option (B) is , which is equivalent to our factored expression.Option (C) is , which is not equivalent because it suggests that both terms originally had an factor, which is not the case.Option (D) is , which is also not equivalent because it suggests that both terms originally had an factor, which is not the case.
More problems from Identify equivalent linear expressions
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help