AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
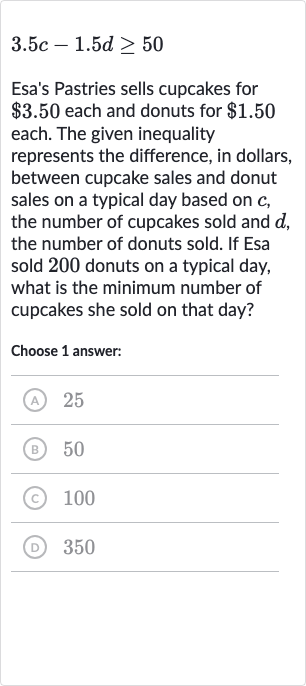
Esa's Pastries sells cupcakes for each and donuts for each. The given inequality represents the difference, in dollars, between cupcake sales and donut sales on a typical day based on , the number of cupcakes sold and , the number of donuts sold. If Esa sold donuts on a typical day, what is the minimum number of cupcakes she sold on that day?Choose answer:(A) (B) (C) (D)
Full solution
Q. Esa's Pastries sells cupcakes for each and donuts for each. The given inequality represents the difference, in dollars, between cupcake sales and donut sales on a typical day based on , the number of cupcakes sold and , the number of donuts sold. If Esa sold donuts on a typical day, what is the minimum number of cupcakes she sold on that day?Choose answer:(A) (B) (C) (D)
- Substitute Value of : Substitute the value of into the inequality.Given the inequality and knowing that Esa sold donuts, we substitute with .
- Perform Multiplication: Perform the multiplication.Calculate to find the total sales from donuts.
- Isolate Term with c: Isolate the term with c.Add to both sides of the inequality to isolate the term with c.
- Solve for c: Solve for c.Divide both sides of the inequality by to find the minimum number of cupcakes .
- Perform Division: Perform the division.Calculate divided by to find the minimum number of cupcakes.
