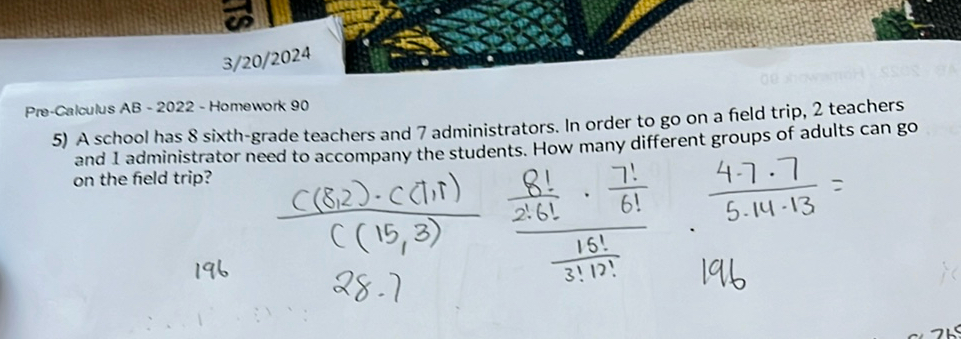A school has 8 sixth-grade teachers and 7 administrators. In order to go on a field trip, 2 teachers and 1 administrator need to accompany the students. How many different groups of adults can go on the field trip?

Question

Bytelearn · Accepted Answer

Calculate Teachers Combination: To find the number of different groups of adults that can go on the field trip, we need to calculate the number of ways to choose 2 teachers out of 8 and 1 administrator out of 7. This is a combination problem where order does not matter.Calculate Administrators Combination: First, calculate the number of ways to choose 2 teachers out of 8. This is given by the combination formula C(n, k) = n! / (k!(n-k)!), where n is the total number and k is the number chosen. So, C(8, 2) = 8! / (2!(8-2)!) = 8! / (2!6!).Multiply Teachers and Administrators: Perform the calculation for C(8, 2). We have 8! / (2!6!) = (8*7*6!)/(2*1*6!) = (8*7)/(2*1) = 28. So there are 28 ways to choose 2 teachers.Incorrect Approach Explanation: Next, calculate the number of ways to choose 1 administrator out of 7. This is given by C(7, 1) = 7! / (1!(7-1)!) = 7! / (1!6!) = 7.Since the selection of teachers and administrators are independent events, we multiply the number of ways to choose the teachers by the number of ways to choose the administrator. So, the total number of different groups is 28 (from the teachers) * 7 (from the administrators) = 196.The given expression (c(8,2)*c(1,1))/(c(15,3))((8!)/(2!6!)*(7!)/(6!))/((15!)/(3!12!))*(4*7*7)/(5*14*13) seems to be an incorrect approach to the problem and includes unnecessary calculations. The correct approach is simply to multiply the combinations of teachers and administrators as calculated in the previous steps.

A school has $8$ sixth-grade teachers and $7$ administrators. In order to go on a field trip, $2$ teachers and $1$ administrator need to accompany the students. How many different groups of adults can go on the field trip?

Full solution

More problems from Identify equivalent linear expressions: word problems

Related topics

A school has 888 sixth-grade teachers and 777 administrators. In order to go on a field trip, 222 teachers and 111 administrator need to accompany the students. How many different groups of adults can go on the field trip?

A school has $8$ sixth-grade teachers and $7$ administrators. In order to go on a field trip, $2$ teachers and $1$ administrator need to accompany the students. How many different groups of adults can go on the field trip?