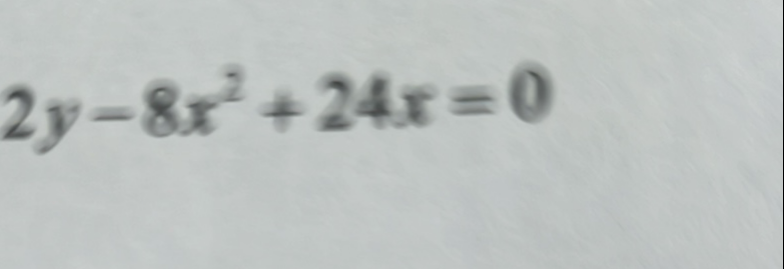2y-8x^(2)+24 x=0

Question

2y-8x^(2)+24 x=0

Bytelearn · Accepted Answer

Identify Terms: Step Title: Identify the Terms Concise Step Description: Identify the terms of the equation and rearrange them if necessary. Step Calculation: The terms are 2y, -8x^2, and 24x. We can rearrange the equation to group like terms or to make it easier to factor by common terms. Step Output: Terms: 2y, -8x^2, 24xFactor by Grouping: Step Title: Factor by Grouping Concise Step Description: Factor by grouping terms that have common factors. Step Calculation: We can factor out a 2 from the entire equation to simplify it: 2(y - 4x^2 + 12x). Step Output: Factored Equation: 2(y - 4x^2 + 12x)Factor Quadratic Expression: Step Title: Factor the Quadratic Expression Concise Step Description: Factor the quadratic expression within the parentheses. Step Calculation: We need to find factors of -4x^2 and 12x that can be grouped. However, since y is not a term that can be combined with x terms, we cannot factor the quadratic expression in the usual way. Instead, we can only factor out common factors of the x terms. Step Output: Factored Equation: 2(y - 4x(x - 3))Check Further Factoring: Step Title: Check for Further Factoring Concise Step Description: Check if the expression can be factored further. Step Calculation: The expression 2(y - 4x(x - 3)) cannot be factored further since y and x are not like terms. Step Output: Final Factored Equation: 2(y - 4x(x - 3))

$2 y-8 x^{2}+24 x=0$

Full solution

More problems from Factor polynomials

Related topics

2y−8x2+24x=0 2 y-8 x^{2}+24 x=0 2y−8x2+24x=0

$2 y-8 x^{2}+24 x=0$