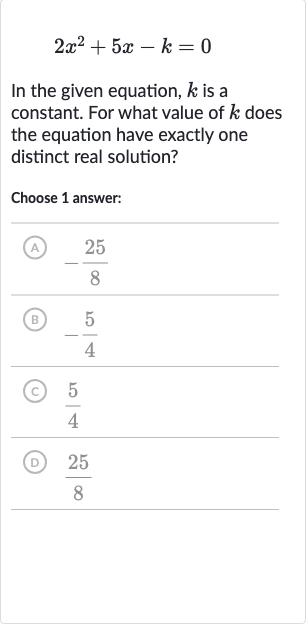
Full solution
Q. In the given equation, is a constant. For what value of does the equation have exactly one distinct real solution?Choose answer:(A) (B) (C) (D)
- Quadratic Equation Discriminant: A quadratic equation has exactly one distinct real solution when its discriminant is equal to zero. This is because the discriminant determines the nature of the roots of the quadratic equation.
- Given Equation and Variables: For the given equation , , , and . We will set the discriminant equal to zero and solve for .
Discriminant: - Substitute Values: Substitute the values of , , and into the discriminant equation:
- Simplify Equation: Simplify the equation:
- Solve for k: Solve for k:
- Final Solution: The value of for which the equation has exactly one distinct real solution is .