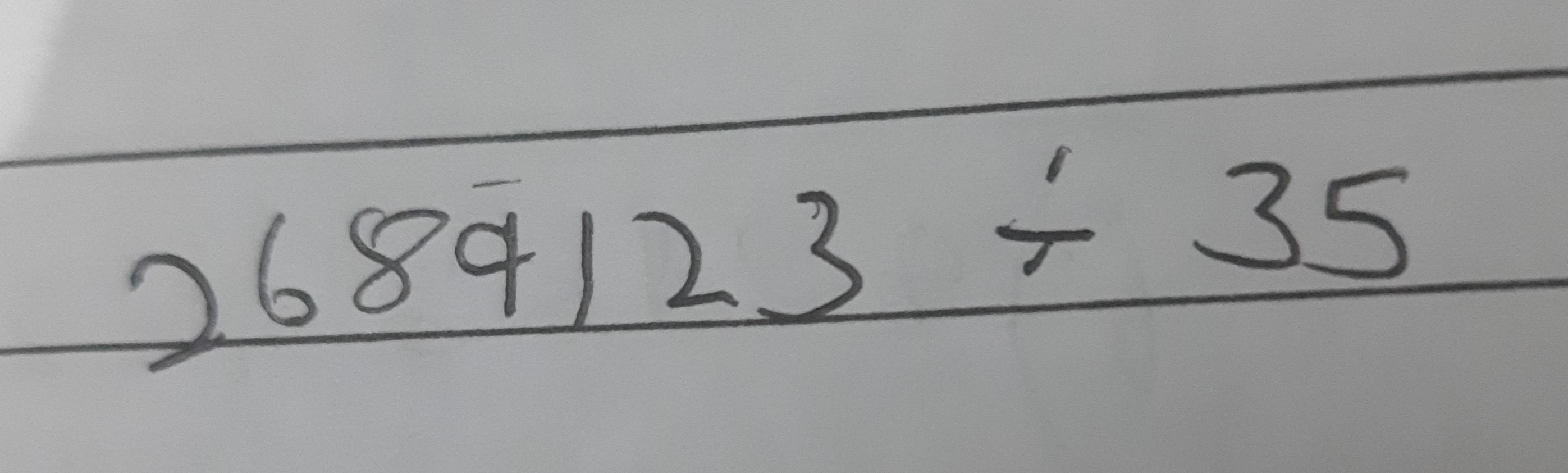AI tutor
Full solution
Q.
- Set up division: Set up the long division of by . To solve , we will use long division.
- Determine first division: Determine how many times goes into the first two digits of , which is . does not go into , so we will consider the first three digits, which is .
- Find remainder: Determine how many times goes into . goes into a total of times because , which is the closest multiple of that does not exceed .
- Bring down next digit: Subtract from to find the remainder..
- Determine next division: Bring down the next digit from the dividend, which is , to make the new number .
- Find next remainder: Determine how many times goes into . goes into a total of times because , which is the closest multiple of that does not exceed .
- Bring down next digit: Subtract from to find the remainder..
- Determine next division: Bring down the next digit from the dividend, which is , to make the new number .
- Find next remainder: Determine how many times goes into . goes into a total of times because , which is the closest multiple of that does not exceed .
- Bring down next digit: Subtract from to find the remainder..
- Determine final division: Bring down the next digit from the dividend, which is , to make the new number .
- Find final remainder: Determine how many times goes into . goes into a total of times because , which is the closest multiple of that does not exceed .
- Find final remainder: Determine how many times goes into . goes into a total of times because , which is the closest multiple of that does not exceed . Subtract from to find the remainder..
- Find final remainder: Determine how many times goes into . goes into a total of times because , which is the closest multiple of that does not exceed . Subtract from to find the remainder.. Bring down the next digit from the dividend, which is , to make the new number .
- Find final remainder: Determine how many times goes into . goes into a total of times because , which is the closest multiple of that does not exceed . Subtract from to find the remainder. . Bring down the next digit from the dividend, which is , to make the new number . Determine how many times goes into . goes into a total of times because , which is the closest multiple of that does not exceed .
- Find final remainder: Determine how many times goes into . goes into a total of times because , which is the closest multiple of that does not exceed . Subtract from to find the remainder.. Bring down the next digit from the dividend, which is , to make the new number . Determine how many times goes into . goes into a total of times because , which is the closest multiple of that does not exceed . Subtract from to find the remainder.. This is the final remainder since there are no more digits to bring down.