AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
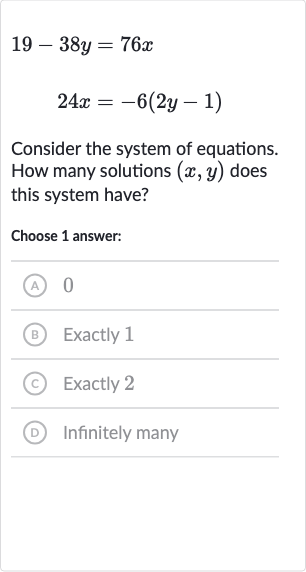
Consider the system of equations. How many solutions does this system have?Choose answer:(A) (B) Exactly (C) Exactly (D) Infinitely many
Full solution
Q. Consider the system of equations. How many solutions does this system have?Choose answer:(A) (B) Exactly (C) Exactly (D) Infinitely many
- Simplify first equation: First, let's simplify each equation to see if we can find a relationship between and . Starting with the first equation: We can divide both sides by to simplify: Now, let's isolate :
- Isolate in first equation: Next, let's simplify the second equation:We can distribute the :Now, let's isolate :
- Simplify second equation: Now we have two expressions for :Let's set them equal to each other to see if there is a solution for that satisfies both equations:
- Isolate y in second equation: To solve for x, we can multiply both sides by to get rid of the denominators:Now, let's add x to both sides:Then, add to both sides:Now, divide both sides by :
- Set equations equal to each other: Now that we have the value for , let's substitute it back into one of the expressions for to find the corresponding value:
