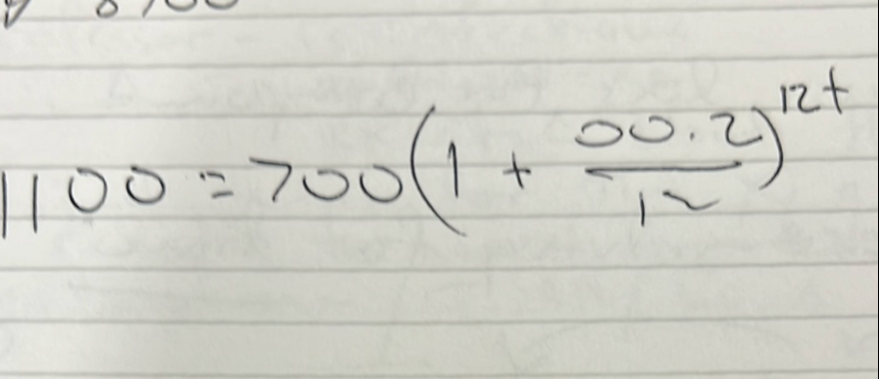AI tutor
Full solution
Q.
- Isolate exponential part: First, let's isolate the exponential part of the equation by dividing both sides by .
- Calculate left side: Now, let's calculate the left side of the equation.
- Take natural logarithm: Next, we need to take the natural logarithm () of both sides to solve for .
- Rewrite right side: Using the property of logarithms that , we can rewrite the right side of the equation.
- Calculate natural logarithm: Now, let's calculate the natural logarithm of both sides.
- Solve for t: We can now solve for by dividing both sides by .
- Calculate value of t: Finally, let's calculate the value of .
More problems from Find trigonometric functions using a calculator
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help