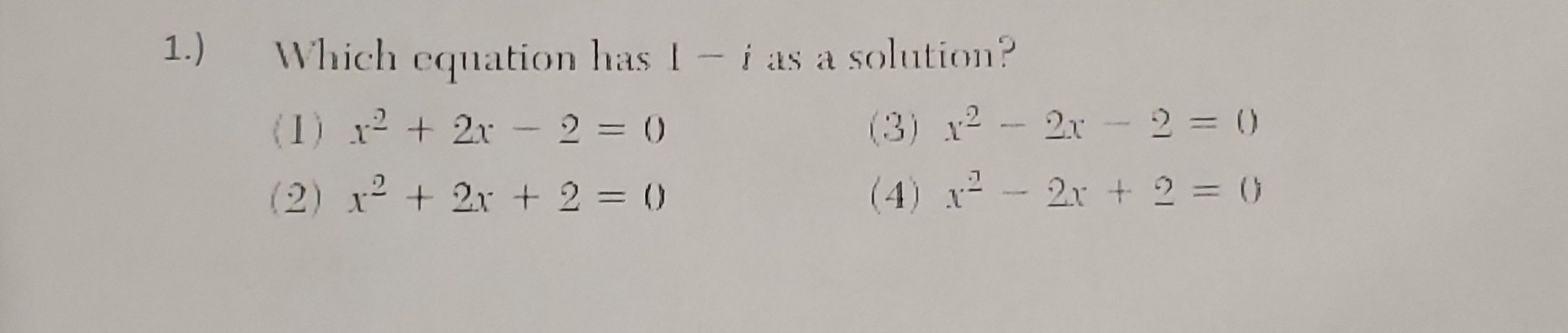1.) Which equation has 1 - i as a solution? (1) x^(2)+2x-2=0 (3) x^(2)-2x-2=0 (2) x^(2)+2x+2=0 (4) x^(2)-2x+2=0

Question

1.) Which equation has 1 - i as a solution? (1)  x^(2)+2x-2=0 (3)  x^(2)-2x-2=0 (2)  x^(2)+2x+2=0 (4)  x^(2)-2x+2=0

Bytelearn · Accepted Answer

Understand the Problem: Step Title: Understand the Problem Concise Step Description: Determine what is being asked in the problem. Question Prompt: Which equation has 1 - i as a solution?Apply Conjugate Root Theorem: Step Title: Apply the Conjugate Root Theorem Concise Step Description: Use the Conjugate Root Theorem, which states that if a polynomial has real coefficients and a complex number a + bi is a root, then its conjugate a - bi is also a root. Calculation: Since 1 - i is a root, the conjugate 1 + i must also be a root.Test Each Equation: Step Title: Test Each Equation Concise Step Description: Substitute 1 - i into each equation to see which one is satisfied. Calculation for Equation (1): (1 - i)^2 + 2(1 - i) - 2 = 0 Calculation: (1 - 2i + i^2) + 2 - 2i - 2 = 0 Calculation: (1 - 2i - 1) + 2 - 2i - 2 = 0 Calculation: -2i + 2 - 2i = 0 Calculation: -4i + 2 ≠ 0

$1$ .) Which equation has $1$ - $i$ as a solution? $\newline$ ( $1$ ) $x^{2}+2 x-2=0$ $\newline$ ( $3$ ) $x^{2}-2 x-2=0$ $\newline$ ( $2$ ) $x^{2}+2 x+2=0$ $\newline$ ( $4$ ) $x^{2}-2 x+2=0$

Full solution

More problems from Factor polynomials

Related topics

111.) Which equation has 111 - iii as a solution?\newline(111) x2+2x−2=0 x^{2}+2 x-2=0 x2+2x−2=0\newline(333) x2−2x−2=0 x^{2}-2 x-2=0 x2−2x−2=0\newline(222) x2+2x+2=0 x^{2}+2 x+2=0 x2+2x+2=0\newline(444) x2−2x+2=0 x^{2}-2 x+2=0 x2−2x+2=0

$1$ .) Which equation has $1$ - $i$ as a solution? $\newline$ ( $1$ ) $x^{2}+2 x-2=0$ $\newline$ ( $3$ ) $x^{2}-2 x-2=0$ $\newline$ ( $2$ ) $x^{2}+2 x+2=0$ $\newline$ ( $4$ ) $x^{2}-2 x+2=0$