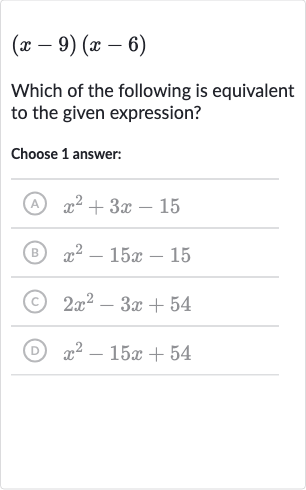
Full solution
Q. Which of the following is equivalent to the given expression?Choose answer:(A) (B) (C) (D)
- Use Distributive Property: To find the equivalent expression for the product , we will use the distributive property (also known as the FOIL method for binomials) to expand the expression. This involves multiplying each term in the first binomial by each term in the second binomial.
- Multiply First Terms: First, we multiply the first terms of each binomial: .
- Multiply Outer Terms: Next, we multiply the outer terms: .
- Multiply Inner Terms: Then, we multiply the inner terms: .
- Multiply Last Terms: Finally, we multiply the last terms of each binomial: .
- Combine Like Terms: Now, we combine the like terms ( and ) to get the final expanded expression: .
- Simplify Expression: Simplifying the expression by combining the like terms, we get: .
- Compare with Answer Choices: Comparing the simplified expression with the answer choices, we find that it matches with choice (D) .
More problems from Identify equivalent linear expressions I
QuestionGet tutor help