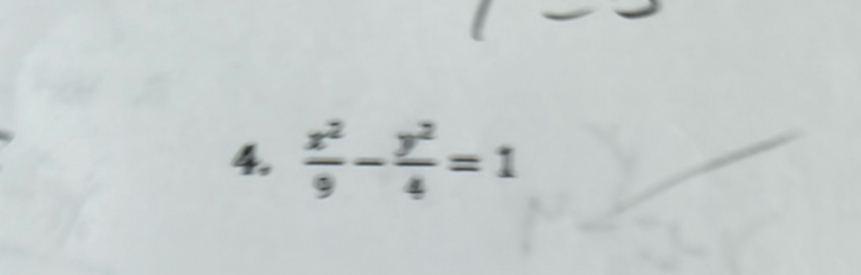AI tutor
Full solution
Q. .
- Identify Equation Type: Identify the type of equation.The given equation is in the form of a hyperbola equation.
- Rewrite in Standard Form: Rewrite the equation in standard form.The standard form of a hyperbola equation is where and are real numbers.
- Compare with Standard Form: Compare the given equation with the standard form.In the given equation , we can see that and .
- Find Values of and : Find the values of and . Taking square roots, we get and .
- Write Final Standard Form: Write the final standard form of the equation.The standard form of the given equation is (\frac{x^\(2\)}{\(3\)^\(2\)} - \frac{y^\(2\)}{\(2\)^\(2\)} = \(1)\.
More problems from Evaluate rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help