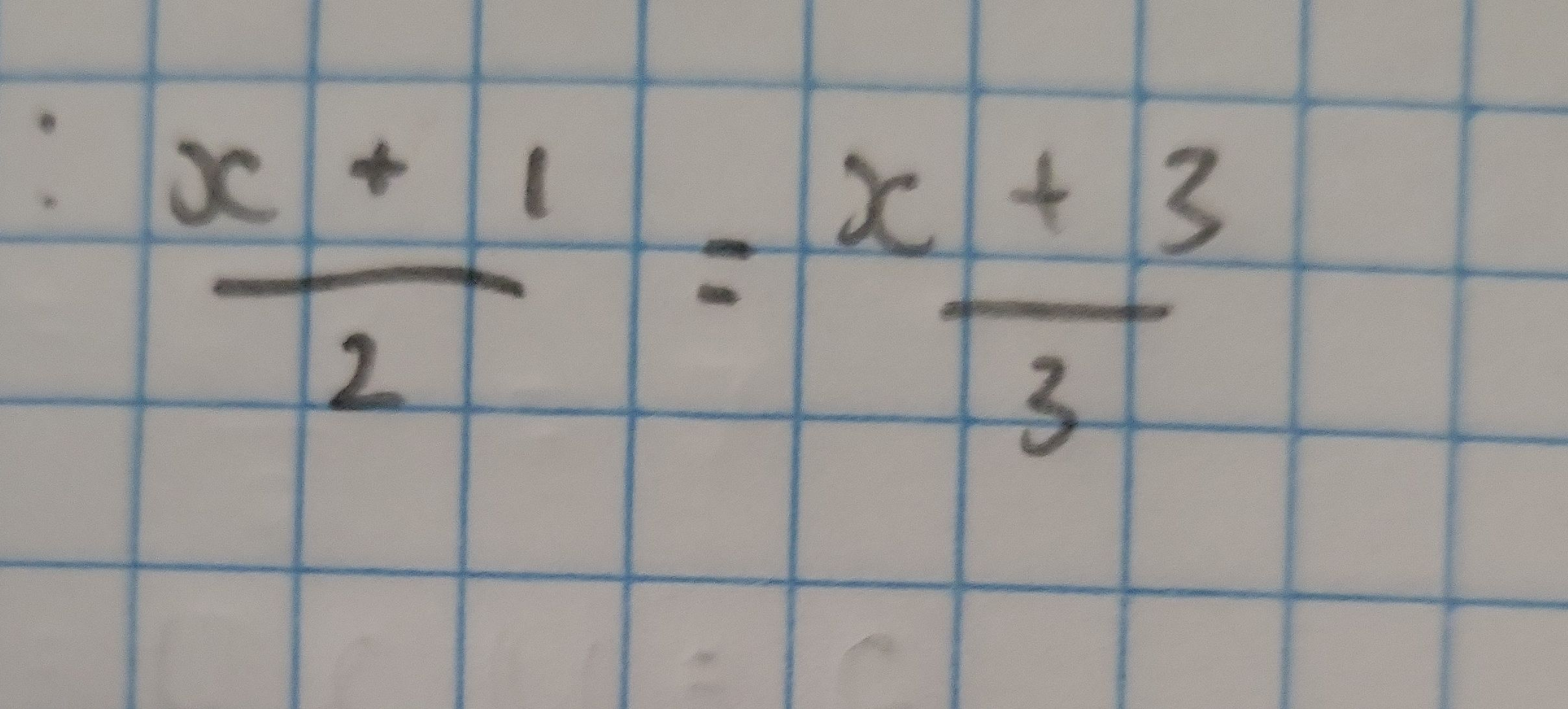AI tutor
Full solution
Q. Solve for .
- Find Common Denominator: To solve the equation , we need to find a common denominator to combine the fractions. The common denominator for and is . We will multiply both sides of the equation by to eliminate the denominators.
- Multiply by : After multiplying both sides by , we distribute the to the numerators on both sides of the equation.This simplifies to:
- Distribute : Now we distribute the and the into the parentheses.
- Distribute and : Next, we want to get all the terms on one side and the constants on the other side. We can do this by subtracting from both sides and subtracting from both sides.
- Combine Like Terms: Simplifying both sides of the equation gives us:
More problems from Add and subtract linear expressions
QuestionGet tutor help