Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

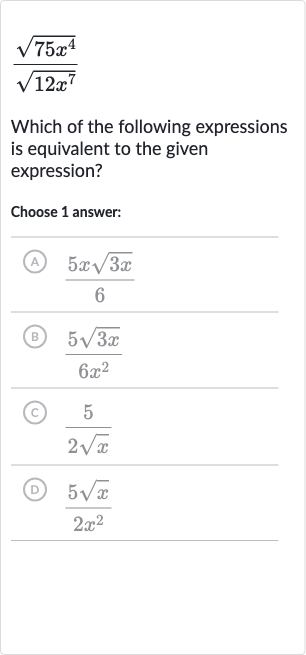
(sqrt(75x^(4)))/(sqrt(12x^(7))) Which of the following expressions is equivalent to the given expression? Choose 1 answer: (A) (5xsqrt(3x))/(6) (B) (5sqrt(3x))/(6x^(2)) (C) (5)/(2sqrtx) (D) (5sqrtx)/(2x^(2))

75x412x7 \frac{\sqrt{75 x^{4}}}{\sqrt{12 x^{7}}} \newlineWhich of the following expressions is equivalent to the given expression?\newlineChoose 11 answer:\newline(A) 5x3x6 \frac{5 x \sqrt{3 x}}{6} \newline(B) 53x6x2 \frac{5 \sqrt{3 x}}{6 x^{2}} \newline(C) 52x \frac{5}{2 \sqrt{x}} \newline(D) 5x2x2 \frac{5 \sqrt{x}}{2 x^{2}}

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Grade 7right chevron icon
Identify equivalent linear expressions Iright chevron icon

Full solution

Q. 75x412x7 \frac{\sqrt{75 x^{4}}}{\sqrt{12 x^{7}}} \newlineWhich of the following expressions is equivalent to the given expression?\newlineChoose 11 answer:\newline(A) 5x3x6 \frac{5 x \sqrt{3 x}}{6} \newline(B) 53x6x2 \frac{5 \sqrt{3 x}}{6 x^{2}} \newline(C) 52x \frac{5}{2 \sqrt{x}} \newline(D) 5x2x2 \frac{5 \sqrt{x}}{2 x^{2}}
  1. Simplify square roots: Simplify the square roots separately.\newlineWe have the expression 75x412x7\frac{\sqrt{75x^{4}}}{\sqrt{12x^{7}}}. We can simplify the square roots by factoring out perfect squares.\newline75x4=25⋅3⋅x4=25⋅3⋅x4=5x23\sqrt{75x^{4}} = \sqrt{25\cdot 3\cdot x^{4}} = \sqrt{25}\cdot\sqrt{3}\cdot\sqrt{x^{4}} = 5x^2\sqrt{3}\newline12x7=4⋅3⋅x6⋅x=4⋅3⋅x6⋅x=2x33x\sqrt{12x^{7}} = \sqrt{4\cdot 3\cdot x^{6}\cdot x} = \sqrt{4}\cdot\sqrt{3}\cdot\sqrt{x^{6}}\cdot\sqrt{x} = 2x^3\sqrt{3}\sqrt{x}
  2. Divide simplified square roots: Divide the simplified square roots.\newlineNow we divide the expressions we found in Step 11.\newline(5x232x33x)(\frac{5x^2\sqrt{3}}{2x^3\sqrt{3}\sqrt{x}})
  3. Cancel out common terms: Cancel out common terms.\newlineThe 3\sqrt{3} terms cancel out, and we can simplify the xx terms by subtracting the exponents.\newline5x22x3x\frac{5x^2}{2x^3\sqrt{x}}\newline= 52xx\frac{5}{2x\sqrt{x}}
  4. Rationalize the denominator: Rationalize the denominator.\newlineTo rationalize the denominator, we multiply the numerator and the denominator by x\sqrt{x} to eliminate the square root in the denominator.\newline5x2xxx\frac{5\sqrt{x}}{2x\sqrt{x}\sqrt{x}}\newline= 5x2x2\frac{5\sqrt{x}}{2x^2}
  5. Check the answer choices: Check the answer choices.\newlineNow we compare our simplified expression with the answer choices.\newline(A) (5x3x)/(6)(5x\sqrt{3x})/(6) - Incorrect, as there is no xx term in the numerator.\newline(B) (53x)/(6x2)(5\sqrt{3x})/(6x^{2}) - Incorrect, as there is no 3\sqrt{3} term in the numerator.\newline(C) (5)/(2x)(5)/(2\sqrt{x}) - Incorrect, as the denominator is not rationalized.\newline(D) (5x)/(2x2)(5\sqrt{x})/(2x^{2}) - Correct, as it matches our simplified expression.

More problems from Identify equivalent linear expressions I

Question
Simplify the expression:\newline7z2+3z27z^2 + 3z^2 \newline ______
Get tutor helpright-arrow

Posted 7 months ago

Question
Simplify the expression:\newline10f+8f−9f−6f10f + 8f - 9f - 6f\newline____
Get tutor helpright-arrow

Posted 7 months ago

Question
Subtract.\newline(3h+6)−(3h+2)(3h + 6) - (3h + 2)\newline____
Get tutor helpright-arrow

Posted 7 months ago

Question
Simplify the expression:\newline2p−p2p - p \newline______
Get tutor helpright-arrow

Posted 9 months ago

Question
A school charges $6\$6 per ticket to a dance. They spend $300\$300 on music and decorations. The expression 6n−3006n-300 describes the amount of profit the school makes from the dance if nn students buy tickets. What does 6n6n represent in this context?\newlineChoices:\newline(A)The amount of money the school charges for all `\n` tickets\newline(B)The amount of money the school spends on the dance\newline(C)The number of students who buy tickets\newline(D)The profit the school earns per ticket
Get tutor helpright-arrow

Posted 8 months ago

Question
Which is equal to cos⁡60∘ \cos 60^\circ ? \newlineChoices:\newline(A) sin⁡30∘ \sin 30^\circ \newline(B) sin⁡60∘ \sin 60^\circ \newline(C) cos⁡30∘ \cos 30^\circ \newline(D) cos⁡60∘ \cos 60^\circ
Get tutor helpright-arrow

Posted 10 months ago

Question
Which is equal to sin⁡45∘\sin 45^\circ? \newlineChoices:\newline(A) cos⁡45∘\cos 45^\circ\newline(B) cos⁡55∘\cos 55^\circ\newline(C) sin⁡55∘\sin 55^\circ\newline(D) sin⁡35∘\sin 35^\circ
Get tutor helpright-arrow

Posted 7 months ago

Question
Which is equal to cos⁡75∘\cos 75^\circ? \newlineChoices:\newline(A) sin⁡15∘\sin 15^\circ\newline(B) sin⁡75∘\sin 75^\circ\newline(C) cos⁡15∘\cos 15^\circ\newline(D) cos⁡25∘\cos 25^\circ
Get tutor helpright-arrow

Posted 7 months ago

Question
Which is equal to sin⁡30∘ \sin 30^\circ ? \newlineChoices:\newline(A) cos⁡60∘ \cos 60^\circ \newline(B) cos⁡30∘ \cos 30^\circ \newline(C) sin⁡60∘ \sin 60^\circ \newline(D) sin⁡30∘ \sin 30^\circ
Get tutor helpright-arrow

Posted 7 months ago

Question
Which is equal to cos⁡45∘ \cos 45^\circ ? \newlineChoices:\newline(A) sin⁡45∘ \sin 45^\circ \newline(B) sin⁡55∘ \sin 55^\circ \newline(C) cos⁡55∘ \cos 55^\circ \newline(D) cos⁡35∘ \cos 35^\circ
Get tutor helpright-arrow

Posted 7 months ago

View all (161)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant