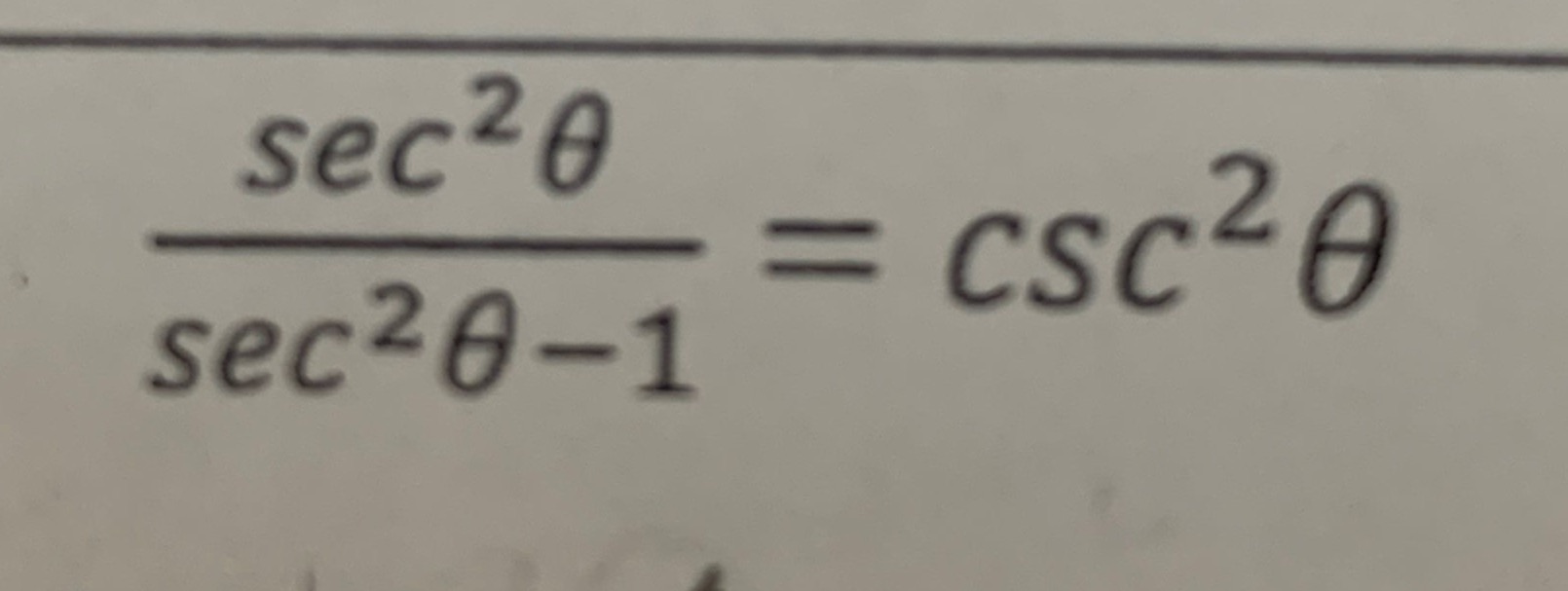AI tutor
Full solution
Q. Simplify:
- Recognize identity: Recognize the trigonometric identity:
- Substitute into equation: Substitute the identity into the equation:
- Simplify expression: Simplify the expression:
- Further simplify using cotangent: Further simplify using the identity for cotangent:
- Use Pythagorean identity: Use the Pythagorean identity for cosecant:
- Substitute back to find relationship: Substitute back to find the relationship:
More problems from Sin, cos, and tan of special angles
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help