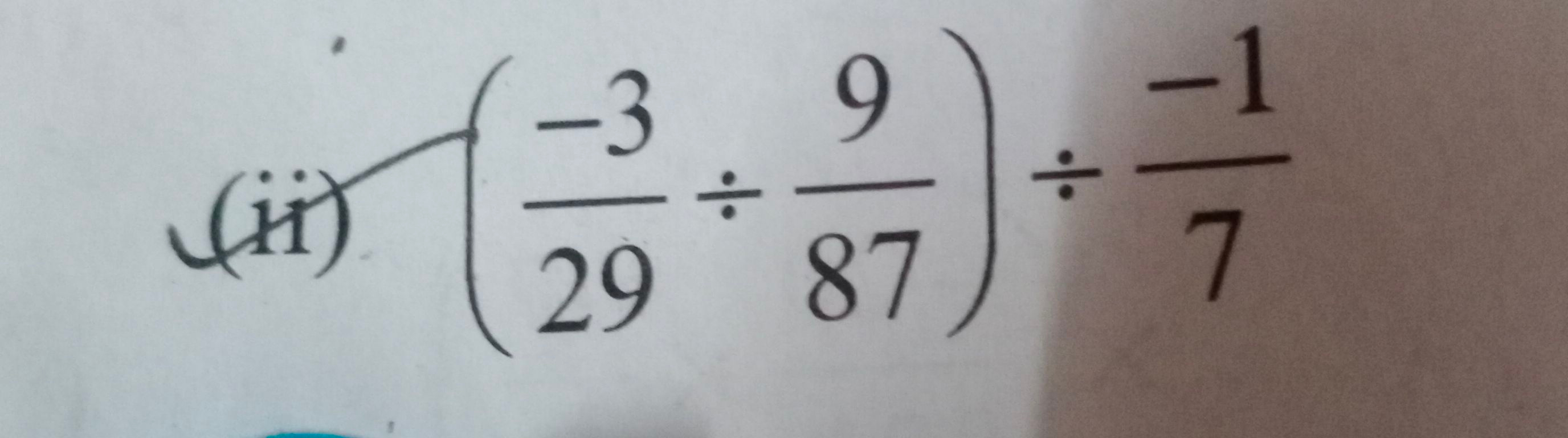AI tutor
Full solution
Q. (ii)
- Simplify Expression: Simplify the expression inside the parentheses.We have the expression . To divide two fractions, we multiply the first fraction by the reciprocal of the second fraction.
- Perform Multiplication: Perform the multiplication.Now we multiply the numerators and the denominators separately.
- Calculate Multiplication: Calculate the multiplication.Calculate the products of the numerators and the denominators.
- Simplify Fraction: Simplify the fraction.Since the numerator and the denominator are the same number (except for the sign), the fraction simplifies to .
- Divide Result: Divide the result by .Now we have to divide by . To do this, we multiply by the reciprocal of .
- Divide Result: Divide the result by . Now we have to divide by . To do this, we multiply by the reciprocal of . Perform the multiplication. Now we multiply the numerators and the denominators separately.
- Divide Result: Divide the result by .Now we have to divide by . To do this, we multiply by the reciprocal of .Perform the multiplication.Now we multiply the numerators and the denominators separately.Calculate the multiplication.Calculate the product of the numerators.
- Divide Result: Divide the result by . Now we have to divide by . To do this, we multiply by the reciprocal of . Perform the multiplication. Now we multiply the numerators and the denominators separately. Calculate the multiplication. Calculate the product of the numerators. Simplify the result. Since dividing by does not change the value, the final result is .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help