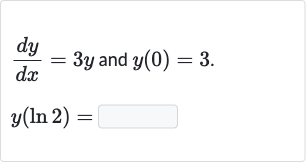(dy)/(dx)=3y and y(0)=3. y(ln 2)=

Question

(dy)/(dx)=3y and  y(0)=3.  y(ln 2)=

Bytelearn · Accepted Answer

Separate variables: First, we need to solve the differential equation (dy)/(dx) = 3y. This is a separable differential equation, so we can separate the variables y and x.Integrate both sides: We move dy to one side and all the x terms to the other side to integrate. So we get (1/y)dy = 3dx.Find integration constant: Now we integrate both sides. The integral of (1/y)dy is ln|y|, and the integral of 3dx is 3x. So we have ln|y| = 3x + C, where C is the integration constant.Find particular solution: We need to find the value of C using the initial condition y(0) = 3. Plugging in the values, we get ln|3| = 3*0 + C, which simplifies to ln(3) = C.Exponentiate both sides: Now we have the particular solution ln|y| = 3x + ln(3). To find y, we exponentiate both sides to get |y| = e^(3x + ln(3)).Drop absolute value: Since y is positive from the initial condition y(0) = 3, we can drop the absolute value to get y = e^(3x) * e^(ln(3)).Simplify exponential term: We simplify e^(ln(3)) to just 3, so the equation becomes y = 3e^(3x).Substitute x value: Now we need to find y(ln(2)). We substitute x with ln(2) to get y(ln(2)) = 3e^(3ln(2)).Simplify exponential term: We use the property of exponents to simplify e^(3ln(2)) to (e^(ln(2)))^3, which is 2^3.Calculate final result: So y(ln(2)) = 3 * 2^3. Calculating 2^3 gives us 8, and multiplying by 3 gives us 24.

$\frac{d y}{d x}=3 y$ and $y(0)=3$ . $\newline$ $y(\ln 2)=$

Full solution

More problems from Simplify variable expressions using properties

Related topics

dydx=3y \frac{d y}{d x}=3 y dxdy​=3y and y(0)=3 y(0)=3 y(0)=3.\newliney(ln⁡2)= y(\ln 2)= y(ln2)=

$\frac{d y}{d x}=3 y$ and $y(0)=3$ . $\newline$ $y(\ln 2)=$