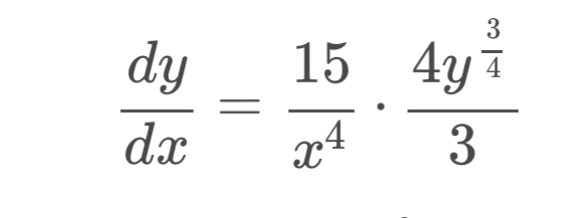AI tutor
Full solution
Q.
- Simplify constants and variables: We are given the differential equation:First, we need to simplify the right-hand side of the equation by multiplying the constants together and keeping the variables separate.
- Combine constants and variables: The constants are and . Multiplying these together gives:Now we have:
- Final simplified form: Next, we simplify the expression by combining the terms with the variables and :This is the simplified form of the given differential equation.
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help