AI tutor
Full solution
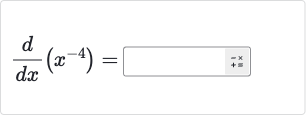
Q.
- Understand Problem: We are asked to find the derivative of the function with respect to . To do this, we will use the power rule for differentiation, which states that the derivative of with respect to is .
- Apply Power Rule: Applying the power rule to , we differentiate as follows: . We subtract from the exponent of .
- Simplify Expression: Simplify the expression:
- Final Derivative: The final simplified form of the derivative is . This is the answer to the problem.