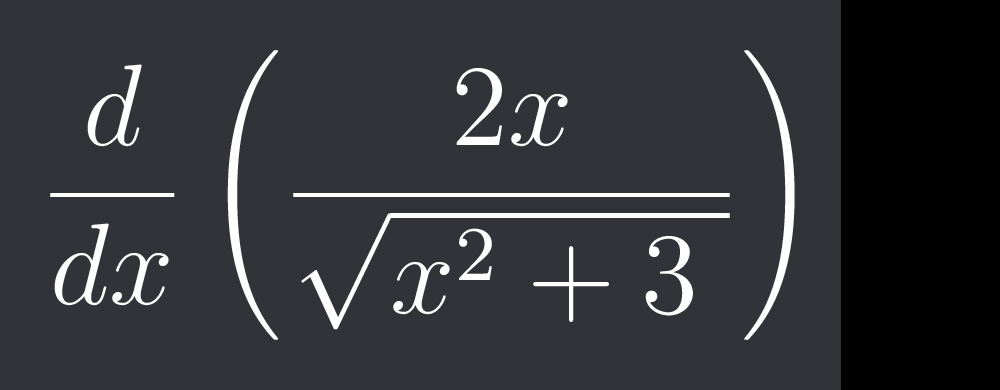AI tutor
Full solution
Q. Find
- Apply Quotient Rule: Use the quotient rule for differentiation, which is , where and .
- Differentiate : Differentiate with respect to to get .
- Differentiate : Differentiate with respect to . First, rewrite as to make it easier.
- Use Chain Rule: Now, use the chain rule to differentiate . The derivative of the outer function with respect to the inner function is . Then multiply by the derivative of the inner function, which is . So, .
- Apply Quotient Rule: Now apply the quotient rule: . Plug in , , , and to get .
- Simplify Numerator: Simplify the numerator: .
- Simplify Denominator: Simplify the denominator: is just .
- Combine Terms: Now, combine the terms in the numerator: .
- Write Final Derivative: Write the final simplified derivative: .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help