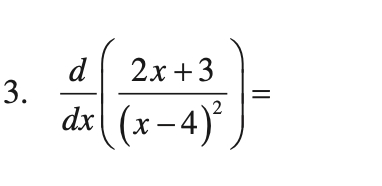AI tutor
Full solution
Q.
- Apply Quotient Rule: To find the derivative of the function , we use the quotient rule which states that if , then . Here, and .
- Find Derivative of : First, find the derivative of . Using the power rule, .
- Find Derivative of : Next, find the derivative of . Using the power rule and chain rule, .
- Simplify Numerator: Apply the quotient rule: .
- Expand and Simplify: Simplify the numerator:.
- Combine Like Terms: Expand and simplify the terms in the numerator:
- Combine Like Terms: Expand and simplify the terms in the numerator:.Combine like terms:..
More problems from Csc, sec, and cot of special angles
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help