AI tutor
Full solution
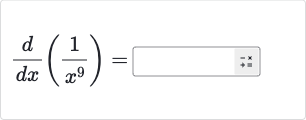
Q.
- Rewrite function: To find the derivative of the function with respect to , we will use the power rule for derivatives. The power rule states that the derivative of with respect to is . In this case, we can rewrite as .
- Apply power rule: Applying the power rule, we take the exponent and multiply it by the function, then subtract from the exponent to get the new power. So the derivative of is or .
- Simplify expression: Simplify the expression to get the final answer. Since is the same as , the final derivative is .