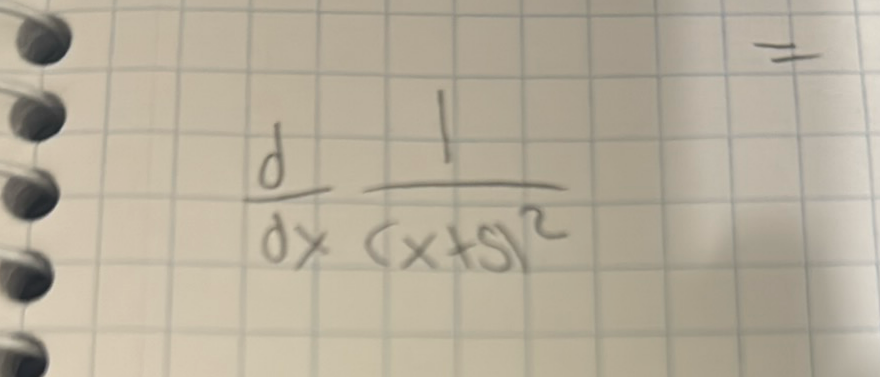AI tutor
Full solution
Q.
- Identify Function: We need to find the derivative of the function with respect to . This is a problem involving the derivative of a function in the form of a quotient where the numerator is a constant and the denominator is a variable raised to a power. We will use the chain rule and the power rule to find the derivative.
- Rewrite Function: Let's rewrite the function to make it easier to differentiate. We can write the function as . This is equivalent to the original function but is now in a form that is easier to differentiate using the power rule.
- Apply Power Rule: Now we apply the power rule for differentiation, which states that the derivative of with respect to is . In this case, we have a function of () raised to the power of . So, we will differentiate as if it were .
- Calculate Derivative: Taking the derivative, we get . We have multiplied the exponent by the coefficient and subtracted one from the exponent, following the power rule.
- Rewrite Final Result: Finally, we can rewrite the derivative in a more readable form. The derivative can be written as .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help