Full solution
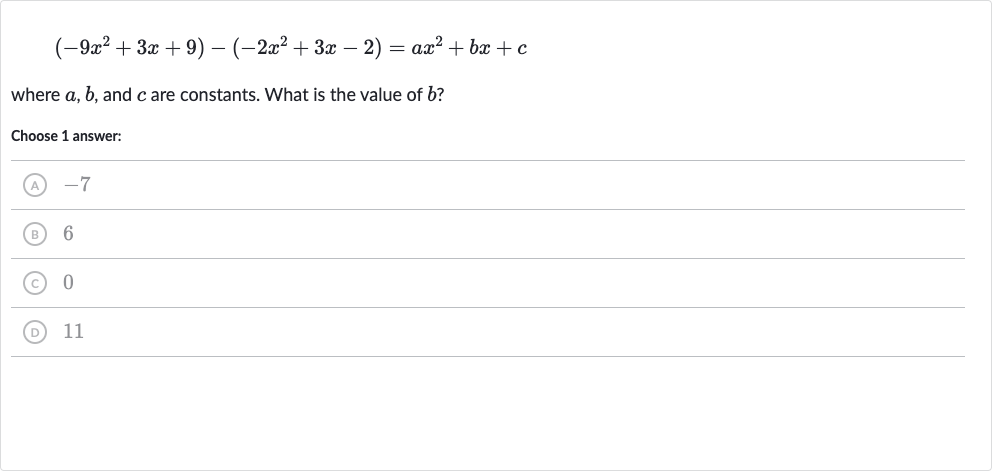
Q. where , and are constants. What is the value of ?Choose answer:(A) (B) (C) (D)
- Distribute negative sign: First, we need to distribute the negative sign to the terms inside the second set of parentheses.=
- Combine like terms: Next, we combine like terms by adding the coefficients of the terms, the terms, and the constant terms separately.
- Identify coefficients: Now we can identify the coefficients , , and in the expression ., , \)
- Find value of : We are asked to find the value of . From our previous step, we have determined that .
More problems from Transformations of quadratic functions
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help