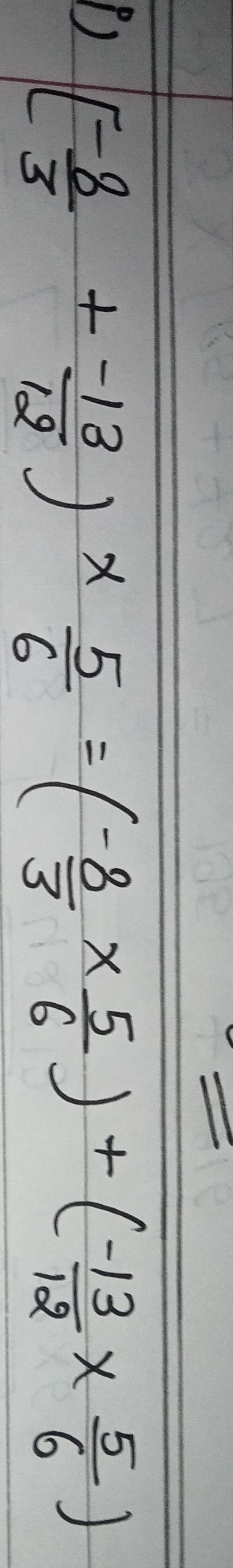Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

[(-8)/(3)+(-13)/(12))×(5)/(6)=(-(8)/(3)×(5)/(6))+(-(13)/(12)×(5)/(6))

11) [−83+−1312)×56=(−83×56)+(−1312×56) \left[\frac{-8}{3}+\frac{-13}{12}\right) \times \frac{5}{6}=\left(-\frac{8}{3} \times \frac{5}{6}\right)+\left(-\frac{13}{12} \times \frac{5}{6}\right)

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Multiplication with rational exponentsright chevron icon

Full solution

Q. 11) [−83+−1312)×56=(−83×56)+(−1312×56) \left[\frac{-8}{3}+\frac{-13}{12}\right) \times \frac{5}{6}=\left(-\frac{8}{3} \times \frac{5}{6}\right)+\left(-\frac{13}{12} \times \frac{5}{6}\right)
  1. Distribute and Simplify: Distribute the multiplication over addition.\newlineWe have the expression [(-8)/(3)+(-13)/(12))\times(5)/(6)]＂). According to the distributive property, we can distribute the multiplication over the addition inside the brackets.\(\newlineSo, \$[(-8)/(3)+(-13)/(12))\times(5)/(6)]\) becomes \([(-(8)/(3)\times(5)/(6))+(-(13)/(12)\times(5)/(6))]\).
  2. Multiply First Term: Multiply the first term.\(\newline\)Now we multiply the first term: \(\left(-\frac{8}{3}\right)\times\frac{5}{6}\).\(\newline\)To multiply fractions, we multiply the numerators together and the denominators together.\(\newline\)So, \(\left(-8\times 5\right) / \left(3\times 6\right) = -\frac{40}{18}\).\(\newline\)We can simplify this fraction by dividing both the numerator and the denominator by their greatest common divisor, which is \(2\).\(\newline\)So, \(-\frac{40}{18}\) simplifies to \(-\frac{20}{9}\).
  3. Multiply Second Term: Multiply the second term.\(\newline\)Now we multiply the second term: \(\left(-\frac{13}{12}\right)\times\frac{5}{6}\).\(\newline\)Again, we multiply the numerators together and the denominators together.\(\newline\)So, \(\left(-13\times 5\right) / \left(12\times 6\right) = -\frac{65}{72}\).\(\newline\)This fraction is already in its simplest form because \(65\) and \(72\) have no common divisors other than \(1\).
  4. Add Simplified Terms: Add the two terms together.\(\newline\)Now we add the two simplified terms: \((-20)/(9) + (-65)/(72)\).\(\newline\)To add fractions, we need a common denominator. The least common multiple of \(9\) and \(72\) is \(72\).\(\newline\)So, we convert \((-20)/(9)\) to have a denominator of \(72\) by multiplying both the numerator and the denominator by \(8\).\(\newline\)\((-20)/(9)\) becomes \((-160)/(72)\).\(\newline\)Now we can add the two fractions: \((-160)/(72) + (-65)/(72) = (-225)/(72)\).
  5. Final Simplification: Simplify the final result.\(\newline\)The fraction \((-225)/(72)\) can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is \(9\).\(\newline\)So, \((-225)/(72)\) simplifies to \((-25)/(8)\).

More problems from Multiplication with rational exponents

Question
Simplify.\newline811281^{\frac{1}{2}}\newline_____________
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify.\newline(−32)1/5(-32)^{1/5}\newline______
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify. Assume all variables are positive.\newlinew43w73\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify. Assume all variables are positive.\newline(2r13)8(2r^{\frac{1}{3}})^8\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify. Assume all variables are positive.\newlinev74⋅v94v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______\newline
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify.\newline114⋅1141^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify. \newline32(−1/5)32^{(-1/5)}
Get tutor helpright-arrow

Posted 7 months ago

Question
Simplify. Assume all variables are positive.\newlinew32w52\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______\newline
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify. Assume all variables are positive.\newline(27x)23(27x)^{\frac{2}{3}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______
Get tutor helpright-arrow

Posted 8 months ago

Question
Simplify. Assume all variables are positive.\newlinex14x114\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______\newline
Get tutor helpright-arrow

Posted 7 months ago

View all (744)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant