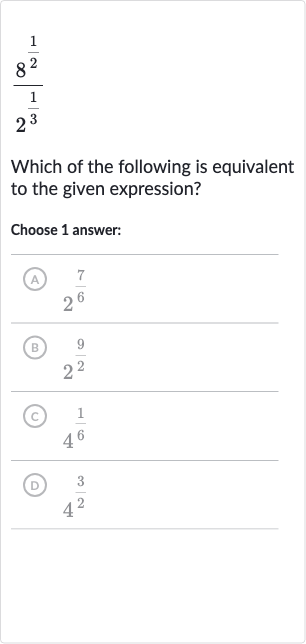
(8^((1)/(2)))/(2^((1)/(3))) Which of the following is equivalent to the given expression? Choose 1 answer: (A) 2^((7)/(6)) (B) 2^((9)/(2)) (C) 4^((1)/(6)) (D) 4^((3)/(2))

Question

(8^((1)/(2)))/(2^((1)/(3))) Which of the following is equivalent to the given expression? Choose 1 answer: (A)  2^((7)/(6)) (B)  2^((9)/(2)) (C)  4^((1)/(6)) (D)  4^((3)/(2))

Bytelearn · Accepted Answer

Simplify using property of exponents: Simplify the expression using the property of exponents that states a^(m/n) = (n√a)^m. (8^(1/2)) can be simplified because 8 is 2^3, so we rewrite the expression as ((2^3)^(1/2))/(2^(1/3)).Apply power of a power rule: Apply the power of a power rule, which states (a^m)^n = a^(m*n). So, ((2^3)^(1/2)) becomes 2^(3*(1/2)) = 2^(3/2).Combine exponents using division property: Now we have the expression 2^(3/2) / 2^(1/3). We can combine the exponents by subtracting the exponent in the denominator from the exponent in the numerator because of the division property of exponents, which states a^m / a^n = a^(m-n). So, 2^(3/2 - 1/3) is our next step.Find common denominator: Find a common denominator to subtract the fractions in the exponents. The common denominator of 2 and 3 is 6, so we convert the fractions: (3/2) = (9/6) and (1/3) = (2/6). Now we subtract the exponents: 2^(9/6 - 2/6).Perform subtraction of exponents: Perform the subtraction of the exponents. 2^(9/6 - 2/6) = 2^(7/6).Match result to answer choices: Match the result to the given answer choices. 2^(7/6) corresponds to choice (A) 2^(7/6).

$\frac{8^{\frac{1}{2}}}{2^{\frac{1}{3}}}$ $\newline$ Which of the following is equivalent to the given expression? $\newline$ Choose $1$ answer: $\newline$ (A) $2^{\frac{7}{6}}$ $\newline$ (B) $2^{\frac{9}{2}}$ $\newline$ (C) $4^{\frac{1}{6}}$ $\newline$ (D) $4^{\frac{3}{2}}$

Full solution

More problems from Identify equivalent linear expressions I

Related topics