Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

find the vertical asymptotes of the function y=sqrt((1-sin x)/(1+sin x))

Find the vertical asymptotes of the functiony=1−sin⁡x1+sin⁡xy=\sqrt{\frac{1-\sin x}{1+\sin x}}

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Precalculusright chevron icon
Solve radical equationsright chevron icon

Full solution

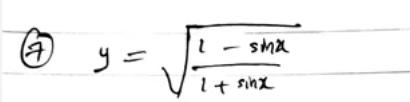
Q. Find the vertical asymptotes of the functiony=1−sin⁡x1+sin⁡xy=\sqrt{\frac{1-\sin x}{1+\sin x}}
  1. Simplify using trigonometric identity: Simplify the expression inside the square root using the trigonometric identity for tangent half-angle.\newlineCalculation: \newlineUsing the identity, (1−sin⁡x)/(1+sin⁡x)=(tan⁡(x/2))2(1 - \sin x) / (1 + \sin x) = (\tan(x/2))^2.
  2. Substitute simplified expression: Substitute the simplified expression back into the original equation.\newlineCalculation:\newliney=(tan⁡(x2))2y = \sqrt{(\tan(\frac{x}{2}))^2}.
  3. Simplify square root: Simplify the square root of a square.\newlineCalculation:\newliney=∣tan⁡(x2)∣y = |\tan(\frac{x}{2})|.

More problems from Solve radical equations

Question
What is the domain of this function? \newliney=xy = \sqrt{x} \newlineChoices: \newline{x∣x≥0}\{x|x \geq 0\}\newline{x∣x≤0}\{x|x \leq 0\}\newline{x∣x<0}\{x | x < 0\}\newline{x∣x>0}\{x|x>0\}
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the real-number root. \newline16\sqrt{16}\newline\newlineWrite your answer in simplified form. \newline____\_\_\_\_
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the real-number root. \newline916\sqrt{\frac{9}{16}}\newlineSimplify your answer and write it as a decimal or as a proper or improper fraction.\newline_____\_\_\_\_\_
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the real-number root using a calculator. Round your answer to the nearest thousandth. \newline`\sqrt{957} `\newline _______
Get tutor helpright-arrow

Posted 2 months ago

Question
Multiply. Write your answer in simplest form. \newline273×42\sqrt{273} \times \sqrt{42}\newline______
Get tutor helpright-arrow

Posted 1 month ago

Question
Simplify. \newline634\sqrt{\frac{63}{4}}\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Simplify. Rationalize the denominator.\newline−49−2\frac{-4}{9 - \sqrt{2}}\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve for z z .\newline16=z 16 = \sqrt{z} \newlinez= z = _____
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve for p p .\newline8=p 8 = \sqrt{p} \newlinep= p = _____
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve for p p .\newline4p=10+3p \sqrt{4p} = \sqrt{10 + 3p} \newlinep= p = _____
Get tutor helpright-arrow

Posted 2 months ago

View all (183)