Full solution
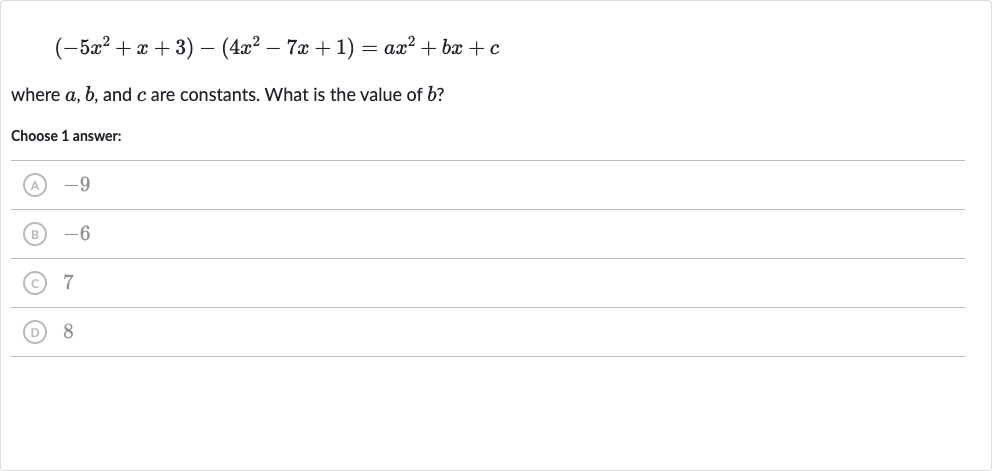
Q. where , and are constants. What is the value of ?Choose answer:(A) (B) (C) (D)
- Subtract and Combine Like Terms: Subtract the second polynomial from the first one by combining like terms.First, combine the terms: Then, combine the terms: Finally, combine the constant terms: So, the expression becomes
- Identify Coefficients: Identify the coefficients of , , and the constant term to find , , and . From the expression , we can see that: , , and
More problems from Transformations of quadratic functions
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help