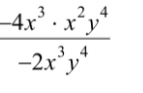Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

(-4x^(3)*x^(2)y^(4))/(-2x^(3)y^(4))

−4x3⋅x2y4−2x3y4 \frac{-4 x^{3} \cdot x^{2} y^{4}}{-2 x^{3} y^{4}} =

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Multiplication with rational exponentsright chevron icon

Full solution

Q. −4x3⋅x2y4−2x3y4 \frac{-4 x^{3} \cdot x^{2} y^{4}}{-2 x^{3} y^{4}} =
  1. Factorize Numerator and Denominator: First, let's factorize the numerator and the denominator.\newlineNumerator: −4x3⋅x2⋅y4=−4x3+2y4=−4x5y4-4x^{3}\cdot x^{2}\cdot y^{4} = -4x^{3+2}y^{4} = -4x^{5}y^{4}\newlineDenominator: −2x3y4-2x^{3}y^{4}
  2. Simplify by Dividing: Next, simplify the expression by dividing the numerator by the denominator.\newline(−4x5y4)/(−2x3y4)=(4/2)⋅(x5−3)⋅(y4−4)(-4x^{5}y^{4})/(-2x^{3}y^{4}) = (4/2)\cdot(x^{5-3})\cdot(y^{4-4})\newline=2x2y0= 2x^{2}y^{0}
  3. Further Simplification: Since y0y^{0} equals 11, we can simplify further:\newline2x2⋅1=2x22x^{2}\cdot1 = 2x^{2}

More problems from Multiplication with rational exponents

Question
Simplify.\newline811281^{\frac{1}{2}}\newline_____________
Get tutor helpright-arrow

Posted 2 months ago

Question
Simplify.\newline(−32)1/5(-32)^{1/5}\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Simplify. Assume all variables are positive.\newlinew43w73\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Simplify. Assume all variables are positive.\newline(2r13)8(2r^{\frac{1}{3}})^8\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______
Get tutor helpright-arrow

Posted 1 month ago

Question
Simplify. Assume all variables are positive.\newlinev74⋅v94v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______\newline
Get tutor helpright-arrow

Posted 2 months ago

Question
Simplify.\newline114⋅1141^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}\newline______
Get tutor helpright-arrow

Posted 1 month ago

Question
Simplify. \newline32(−1/5)32^{(-1/5)}
Get tutor helpright-arrow

Posted 1 month ago

Question
Simplify. Assume all variables are positive.\newlinew32w52\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______\newline
Get tutor helpright-arrow

Posted 2 months ago

Question
Simplify. Assume all variables are positive.\newline(27x)23(27x)^{\frac{2}{3}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Simplify. Assume all variables are positive.\newlinex14x114\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______\newline
Get tutor helpright-arrow

Posted 1 month ago

View all (963)