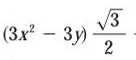Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

(3x^(2)-3y)(sqrt3)/(2)

$\frac{3x^{2}-3y}{2}\sqrt{3}$

View step-by-step help

View step-by-step help

Simplify radical expressions involving fractions

Full solution

Q.

\frac{3x^{2}-3y}{2}\sqrt{3}

Distribute $\sqrt{3}$ : First, distribute the $\sqrt{3}$ to both terms in the parenthesis. $\frac{(3x^{2} \cdot \sqrt{3} - 3y \cdot \sqrt{3})}{2}$
Split into two fractions: Now, split the fraction into two separate fractions. $\newline$ $(\frac{3x^{2} \sqrt{3}}{2}) - (\frac{3y \sqrt{3}}{2})$
Simplify each term: Simplify each term separately. $\frac{3}{2}x^{2} \cdot \sqrt{3} - \frac{3}{2}y \cdot \sqrt{3}$
Write final expression: Write the final simplified expression. $\newline$ $(\frac{3\sqrt{3}}{2})x^{2} - (\frac{3\sqrt{3}}{2})y$

More problems from Simplify radical expressions involving fractions

Question

Multiply. Write your answer in simplest form.

\newline

\sqrt{15} \times \sqrt{2}

\newline

Posted 1 month ago

Question

\newline

\sqrt{125}

Posted 1 month ago

Question

Add. Write your answer in simplest form.

\newline

-6\sqrt{3} + 7\sqrt{3}

\newline

Posted 1 month ago

Question

Multiply. Write your answer in simplest form.

\newline

-\sqrt{2}(5 - \sqrt{5})

Posted 1 month ago

Question

Simplify. Rationalize the denominator.

\newline

`(-7)/(2 + \sqrt{5}\)`

\newline

Posted 1 month ago

Question

Simplify. Assume

x

is greater than or equal to zero.

\newline

\sqrt{20x^3}

Posted 1 month ago

Question

(1+\sqrt{2})^{7}+(1-\sqrt{2})^{7}

Posted 1 month ago

Question

\sqrt{-1} \cdot \sqrt{-1}

Posted 1 month ago

Question

\newline

(\sqrt{i})^{2}

Posted 1 month ago

Question

\int(2x+6)^5\,dx

Posted 1 month ago