Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

(3g-4)(2g-8)=ag^(2)+bg+c
In the given equation,
a,b, and
c are constants. What is the value of
a ?
Choose 1 answer:
(A) -32
(B) -16
(C) 5
(D) 6

$(3 g-4)(2 g-8)=a g^{2}+b g+c$ $\newline$ In the given equation, $a, b$ , and $c$ are constants. What is the value of $a$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $-32$ $\newline$ (B) $-16$ $\newline$ (C) $5$ $\newline$ (D) $6$

View step-by-step help

View step-by-step help

Write a quadratic function from its x-intercepts and another point

Full solution

Q.

(3 g-4)(2 g-8)=a g^{2}+b g+c

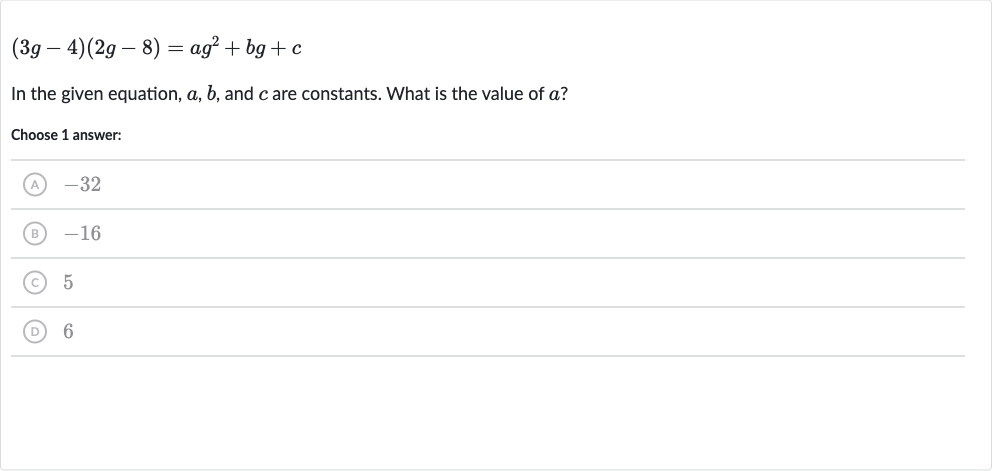
\newline

In the given equation,

a, b

, and

c

are constants. What is the value of

a

?

\newline

Choose

1

answer:

\newline

(A)

-32

\newline

(B)

-16

\newline

(C)

5

\newline

(D)

6

Expand Expression: We need to expand the expression $(3g-4)(2g-8)$ to find the coefficient of the $g^2$ term, which will give us the value of $a$ . Expanding the expression using the distributive property (also known as the FOIL method for binomials): $(3g-4)(2g-8) = 3g \times 2g + 3g \times (-8) + (-4) \times 2g + (-4) \times (-8)$
Perform Multiplication: Now we perform the multiplication for each term: $\newline$ $3g \times 2g = 6g^2$ $\newline$ $3g \times (-8) = -24g$ $\newline$ $(-4) \times 2g = -8g$ $\newline$ $(-4) \times (-8) = 32$
Combine Like Terms: Combine the like terms to get the expanded form: $\newline$ $6g^2 - 24g - 8g + 32$ $\newline$ $6g^2 - 32g + 32$
Find Coefficient: From the expanded form, we can see that the coefficient of $g^2$ is $6$ . This is the value of $a$ .

More problems from Write a quadratic function from its x-intercepts and another point

Question

Solve by completing the square.

\newline

m^2 - 10m - 29 = 0

\newline

Write your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.

\newline

`m` = ____ or `m` = _____

Posted 8 months ago

Question

g(x)

g(x)

is the translation

5

f(x)=x^2

\newline

Write your answer in the form

a(x–h)^2+k

a

h

k

\newline

g(x)=

Posted 7 months ago

Question

What is the range of this quadratic function?

\newline

y = x^2 - 4x + 4

\newline

\newline

\left\{y \mid y \geq 2\right\}

\newline

\left\{y \mid y \leq 0\right\}

\newline

\left\{y \mid y \geq 0\right\}

\newline

\text{all real numbers}

Posted 5 months ago

Question

Write the equation of the parabola that passes through the points

(1,0)

(2,0)

(3,\text{–}16)

. Write your answer in the form

y = a(x – p)(x – q)

a

p

q

are integers, decimals, or simplified fractions.

\newline

Posted 5 months ago

Question

Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic.

\newline

f^2 + 8f + \_\_\_\_\_

Posted 5 months ago

Question

h

\newline

h^2 + 39h = 0

\newline

\newline

Write each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.

\newline

h =

\newline

Posted 5 months ago

Question

Write a quadratic function with zeros

-9

-7

\newline

Write your answer using the variable

x

and in standard form with a leading coefficient of

1

\newline

f(x) = \_\_\_\_\_

Posted 5 months ago

Question

Find the equation of the axis of symmetry for the parabola

y = x^2

\newline

Simplify any numbers and write them as proper fractions, improper fractions, or integers.

\newline

\underline{\hspace{3cm}}

Posted 4 months ago

Question

g(x)

g(x)

is the translation

8

f(x) = x^2

\newline

Write your answer in the form

a(x – h)^2 + k

a

h

k

\newline

g(x) =

\newline

Posted 4 months ago

Question

x

\newline

x^2 = 1

\newline

\newline

Write your answer in simplified, rationalized form.

\newline

x =

x =

\newline

Posted 5 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant