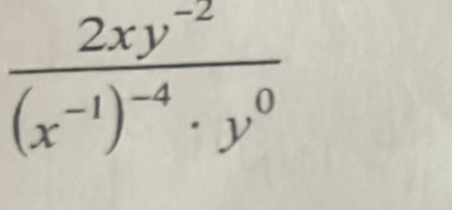AI tutor
Full solution
Q.
- Simplify Denominator: Simplify the denominator.We have in the denominator. According to the power of a power rule, . Also, any number raised to the power of is .So, and .
- Rewrite Expression: Rewrite the expression with the simplified denominator.Now that we have simplified the denominator, we can rewrite the expression as:Since , it does not affect the multiplication and can be omitted.
- Combine Like Terms: Simplify the expression by combining like terms.We have in the numerator and in the denominator. We can simplify the expression by dividing the terms with the same base.
- Rewrite with Positive Exponents: Rewrite the expression with positive exponents.Since we have negative exponents, we can rewrite them with positive exponents by taking the reciprocal of the base.
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help