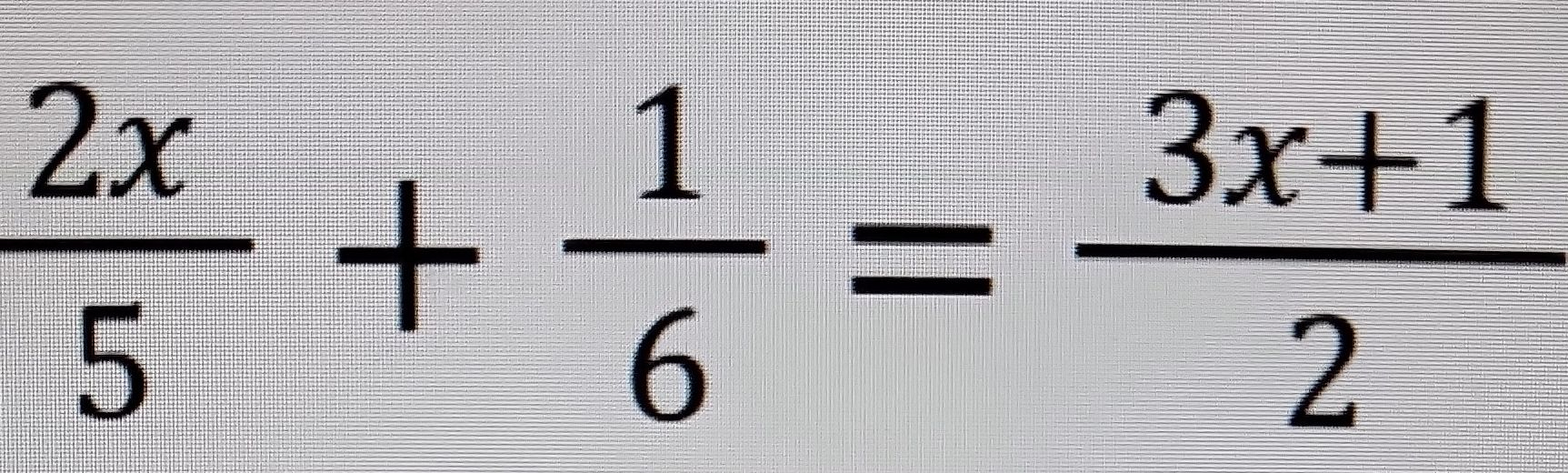Solve for x. (2x)/(5)+(1)/(6)=(3x+1)/(2)

Question

Bytelearn · Accepted Answer

Find Common Denominator: We have the equation (2x)/(5) + (1)/(6) = (3x+1)/(2). The first step is to find a common denominator for the fractions on the left side of the equation to combine them. The least common multiple of 5 and 6 is 30.Convert Fractions to LCD: Convert the fractions (2x)/(5) and (1)/(6) to have the common denominator of 30. This gives us (2x * 6)/(5 * 6) + (1 * 5)/(6 * 5) = (3x+1)/(2).Simplify Fractions: Simplify the fractions to get (12x)/(30) + (5)/(30) = (3x+1)/(2).Combine Fractions: Combine the fractions on the left side of the equation to get a single fraction. This gives us (12x + 5)/(30) = (3x+1)/(2).Cross-Multiply: To solve for x, we can cross-multiply. This means multiplying the numerator of one fraction by the denominator of the other fraction and setting the products equal to each other. So, (12x + 5) * 2 = (3x + 1) * 30.Perform Multiplication: Perform the multiplication to get 24x + 10 = 90x + 30.Isolate x: To isolate x, we need to get all the x terms on one side and the constants on the other. Subtract 24x from both sides to get 10 = 66x + 30.Subtract Constants: Subtract 30 from both sides to get -20 = 66x.Divide by 66: Divide both sides by 66 to solve for x. This gives us x = -20/66.Simplify Fraction: Simplify the fraction -20/66 by dividing both the numerator and the denominator by their greatest common divisor, which is 2. This gives us x = -10/33.

Solve for $x$ . $\newline$ $\frac{2 x}{5}+\frac{1}{6}=\frac{3 x+1}{2}$

Full solution

More problems from Add and subtract linear expressions

Related topics

Solve for xxx.\newline2x5+16=3x+12 \frac{2 x}{5}+\frac{1}{6}=\frac{3 x+1}{2} 52x​+61​=23x+1​

Solve for $x$ . $\newline$ $\frac{2 x}{5}+\frac{1}{6}=\frac{3 x+1}{2}$