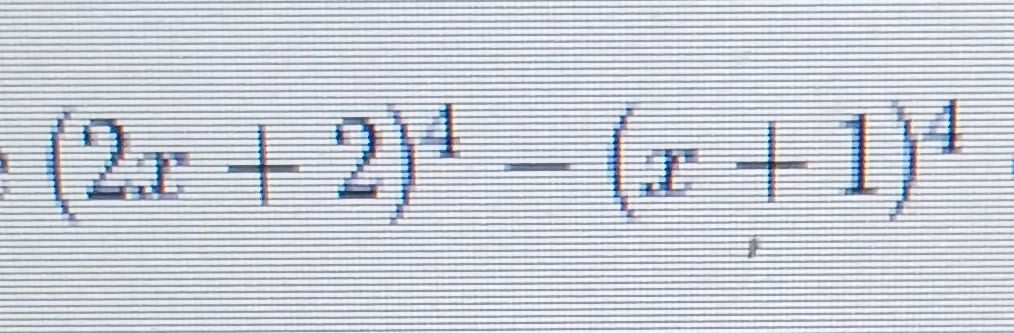Simplify. $\newline$ $(2 x+2)^{4}-(x+1)^{4}$

Full solution

Q. Simplify.

\newline

(2 x+2)^{4}-(x+1)^{4}

Expand Expression: We need to expand both expressions $(2x+2)^{4}$ and $(x+1)^{4}$ using the binomial theorem or by multiplying the binomials step by step.
Expand $(2x+2)^{4}$ : First, let's expand $(2x+2)^{4}$ . This is equivalent to $((2(x+1))^4)$ , which can be simplified by taking the $2^4$ outside the binomial expansion. $\newline$ $(2x+2)^{4} = (2^4) \times (x+1)^{4}$
Factor Out Common Term: Now, we have $(2^4) \cdot (x+1)^{4} - (x+1)^{4}$ . Since $(x+1)^{4}$ is common in both terms, we can factor it out. $(2^4) \cdot (x+1)^{4} - (x+1)^{4} = ((2^4) - 1) \cdot (x+1)^{4}$
Calculate Result: Calculate $2^4$ and subtract $1$ from it. $\newline$ $(2^4) - 1 = 16 - 1 = 15$
Expand $(x+1)^{4}$ : Now, we have $15 \times (x+1)^{4}$ . We need to expand $(x+1)^{4}$ using the binomial theorem or by multiplying the binomial by itself four times.
Apply Binomial Theorem: Expanding $(x+1)^{4}$ using the binomial theorem gives us: $\newline$ $(x+1)^{4} = x^{4} + 4x^{3} + 6x^{2} + 4x + 1$
Multiply by $15$ : Now, multiply the expanded form of $(x+1)^{4}$ by $15$ : $15 \times (x^4 + 4x^3 + 6x^2 + 4x + 1) = 15x^4 + 60x^3 + 90x^2 + 60x + 15$
Final Answer: The final answer is the expanded form of the expression: $15x^4 + 60x^3 + 90x^2 + 60x + 15$