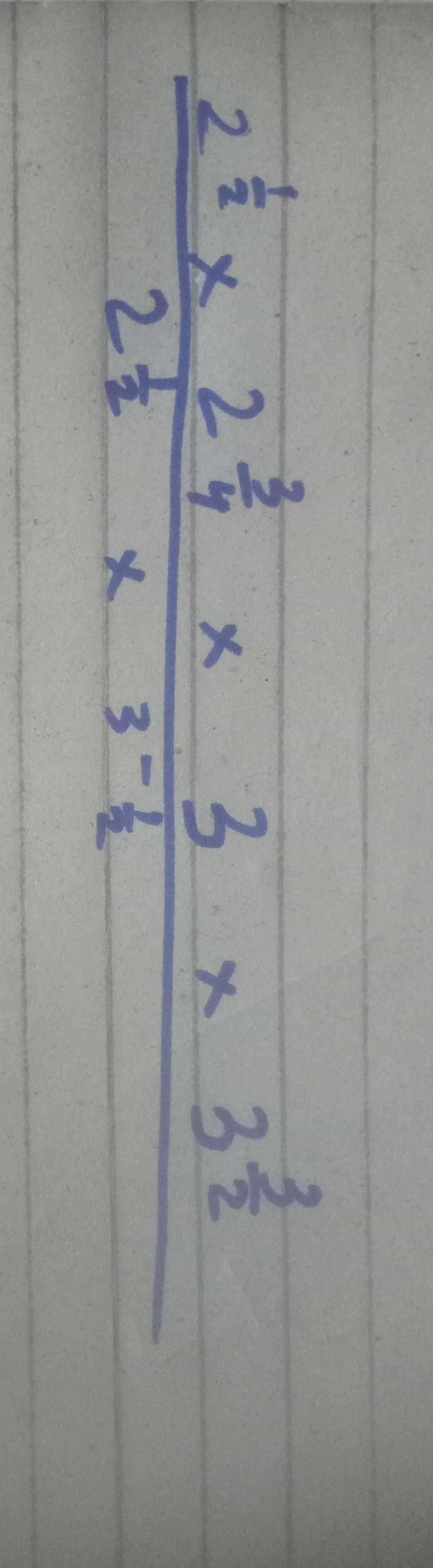Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Simplifying the Expression:(2^((1)/(2))×2^((3)/(4))×3×3^((3)/(2)))/(2^((1)/(2))×3^(-(1)/(2)))

Simplifying the Expression: $\frac{2^{\frac{1}{2}}\times2^{\frac{3}{4}}\times3\times3^{\frac{3}{2}}}{2^{\frac{1}{2}}\times3^{-\frac{1}{2}}}$

View step-by-step help

View step-by-step help

Multiplication with rational exponents

Full solution

Q. Simplifying the Expression:

\frac{2^{\frac{1}{2}}\times2^{\frac{3}{4}}\times3\times3^{\frac{3}{2}}}{2^{\frac{1}{2}}\times3^{-\frac{1}{2}}}

Simplify Bases: Step $1$ : Simplify the numerator and denominator separately by combining like bases. $\newline$ Numerator: $2^{(1/2)} \times 2^{(3/4)} \times 3 \times 3^{(3/2)}$ $\newline$ Denominator: $2^{(1/2)} \times 3^{-(1/2)}$
Combine Exponents: Step $2$ : Apply the property of exponents $a^m \times a^n = a^{m+n}$ to combine the powers of $2$ and $3$ . $\newline$ Numerator: $2^{(1/2 + 3/4)} \times 3^{1 + (3/2)}$ $\newline$ Denominator: $2^{(1/2)} \times 3^{-(1/2)}$
Simplify Exponents: Step $3$ : Simplify the exponents. $\newline$ Numerator: $2^{(5/4)} \times 3^{(5/2)}$ $\newline$ Denominator: $2^{(1/2)} \times 3^{-(1/2)}$
Divide Terms: Step $4$ : Divide the terms with the same base by subtracting the exponents. $\newline$ Result: $\frac{2^{(5/4)}}{2^{(1/2)}} \times \frac{3^{(5/2)}}{3^{-(1/2)}}$
Final Exponents: Step $5$ : Simplify the expression by subtracting the exponents. $\newline$ Result: $2^{(5/4 - 1/2)} \times 3^{(5/2 + 1/2)}$
Calculate Value: Step $6$ : Calculate the final exponents. $\newline$ Result: $2^{(3/4)} \times 3^{3}$
Final Result: Step $7$ : Calculate the numerical value of $3^3$ . $\newline$ Result: $2^{(3/4)} \times 27$

More problems from Multiplication with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 3 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 3 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 3 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 2 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 3 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 2 months ago

Question

\newline

32^{(-1/5)}

Posted 2 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 3 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 2 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 2 months ago