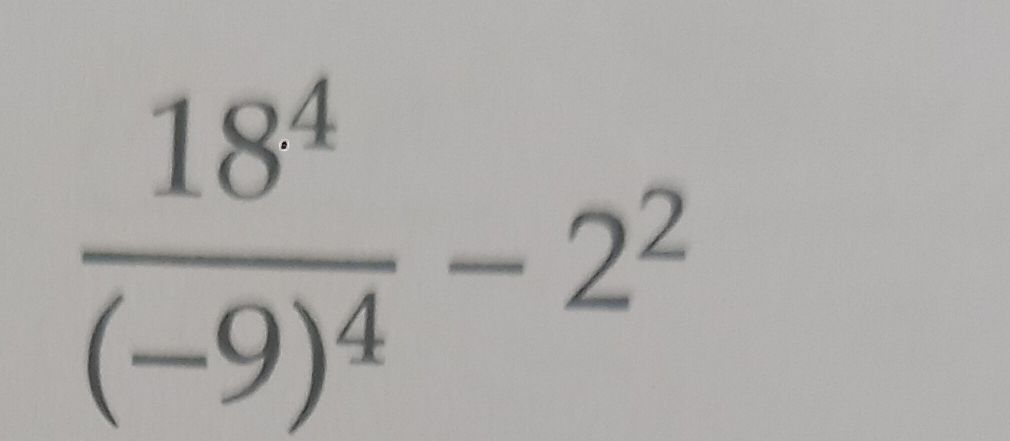Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

(18^(4))/((-9)^(4))-2^(2)

$\frac{18^{4}}{(-9)^{4}}-2^{2}$

View step-by-step help

View step-by-step help

Evaluate rational exponents

Full solution

Q.

\frac{18^{4}}{(-9)^{4}}-2^{2}

Identify base and exponent: Identify the base and the exponent for each term in the expression $(18^{4})/((-9)^{4})-2^{2}$ . $\newline$ In $(18^{4})/((-9)^{4})-2^{2}$ , we have three terms: $\newline$ First term: $18^{4}$ $\newline$ Second term: $(-9)^{4}$ $\newline$ Third term: $2^{2}$
Simplify each term: Simplify each term separately. $\newline$ First term: $18^{4}$ means $18$ multiplied by itself $4$ times. $\newline$ Second term: $(-9)^{4}$ means $-9$ multiplied by itself $4$ times. Since the exponent is even, the result will be positive. $\newline$ Third term: $2^{2}$ means $2$ multiplied by itself once.
Calculate term values: Calculate the value of each term. $\newline$ First term: $18^{4} = 18 \times 18 \times 18 \times 18 = 104976$ $\newline$ Second term: $(-9)^{4} = (-9) \times (-9) \times (-9) \times (-9) = 6561$ $\newline$ Third term: $2^{2} = 2 \times 2 = 4$
Divide first term by second term: Divide the first term by the second term. $\newline$ $(18^{4})/((-9)^{4}) = 104976/6561$
Perform division: Perform the division. $104976/6561 = 16$ (since $6561$ is $9^4$ , and $104976$ is $18^4$ which is $(2\times9)^4$ , so the division simplifies to $(2^4)$ which is $16$ )
Subtract third term: Subtract the third term from the result of the division. $\newline$ $16 - 2^{2} = 16 - 4$
Perform final subtraction: Perform the subtraction to get the final result. $16 - 4 = 12$

More problems from Evaluate rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 9 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 5 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 5 months ago

Question

\newline

32^{(-1/5)}

Posted 7 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant